X^2 y^2 z^2-xy-yz-zx formula 237285

Apply the formula for (ab)²=a²b²2ab for (xy)²,(yz)² & (zx)² and add them together toThe electric potential existing in space is `V(x,y,z)A(xyyzzx)` (a) Write the dimensional formula of A (b) Find the expression for the electric fieAnswered 4 years ago x^2y^2z^2xyyzzx= { (xy)^2} { (yz)^2} { (zx)^2}÷2 sum of squares of three real nos is zero if each is equal to zero so, xy=0, yz=0, zx=0 therefore, x=y=z 23K views Supriyo Ain , Studying in Class 11 Mathematics & Relativity, Hindmotor High School

X 2 Y 2 Z 2 100 Xy Yz Zx 2 Brainly In

X^2 y^2 z^2-xy-yz-zx formula

X^2 y^2 z^2-xy-yz-zx formula-Factor x^2y^2 x2 − y2 x 2 y 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( aRf(P) = h6;10;8i The tangent plane at P has

Arxiv Org

Let us consider LHS of the equation LHS = x 3 y 3 z 3 – 3xyz LHS = 1 3 2 3 3 3 – 3(1 × 2 × 3) LHS = 1 8Use the formula a 3 b 3 c 3 − 3 a b c = ( a b c) ( a 2 b 2 c 2 − a b − b c − c a) = 1 2 ( a b c) ( ( a − b) 2 ( b − c) 2 ( c − a) 2) and then notice that a − b = x 2 − y 2 z x − y z = ( x − y) ( x y z) This will lead you to get the answer as ( x 3 y 3 z 3 − 3 x y z) 2 as pointed out by Ewan Delanoy Share Follow this answer to receive notificationsJACOBIAN Find ꝺ (u,v,w)/ꝺ (x,y,z) where u=x^2 y^2 z^2 v=xyyzzx w=xyz Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting

Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music∂z ∂x = x(x2 y3)9 1 x (Note We used the chain rule on the first term) ∂z ∂y = 30y 2(x y3)9 (Note Chain rule again, and second term has no y) 3 If z = f(x,y) = xexy, then the partial derivatives are ∂z ∂x = exy xyexy (Note Product rule (and chain rule in the second term) ∂z ∂y = x2exy (Note No product rule, but weSolutionShow Solution x y z = 4 and x 2 y 2 z 2 = 30 Since ( x y z)2 = x2 y2 z2 2 ( xy yz zx ), we have (4)2 = 30 2 ( xy yz zx ) ⇒ 16 = 30 2 ( xy yz zx ) ⇒ 2 ( xy yz zx ) = 14 ⇒ xy yz zx = `14/2` = 7 ∴ xy yz zx = 7 Concept Expansion of Formula

, z 1) and (x 2, y 2, z 2) parallel to the coordinate planes The length of edges are x 2 – x 1, y 2 – y 1, z 2 – z 1 and length of diagonal is 2 2 2 ( ) ( ) ( )x x y y z z2 1 2 1 2 1− − − 1215 Section formula The coordinates of the point R which divides the line segment joining two points P(x 1, y 1, z 1) and Q(x 2, y 2, zX³ y³ z³ –3xyz = (xyz)(x 2 y 2 z 2 –xy–yz−xz) x ² y ² =12(xy) ² (x–y) ² (xa)(xb)(xc)=x³ (abc)x² (abbcca)xabc x³ y³ = (xy)(x² – xy y²) x³ – y³=(x–y)(x² xy y²) x² y² z² − xy – yz – zx = 12(x−y)² (y−z)² (z−x)²Arrange the expression in the form of factorization (x y z)(xy yz zx)− xyz ( x y z) ( x y y z z x) − x y z Expand the expression x2y x2z xy2 2xyz xz2 y2z yz2 x 2 y x 2 z x y 2 2 x y z x z 2 y 2 z y z 2 Do factorization (x y)(x z)(y z) ( x y) ( x z) ( y z)

X Y Z 2 X 2 Y 2 Z 2 2 Yz Zx Xy

Prove That X Y Z Xy Yz Zx Is Always Positive Mathematics Topperlearning Com 58pxibcc

Multiply X2 Y2 Z2 − Xy Xz Yz By X Y − ZFor example, x 2 zp y 2 zp = xy and (x 2 – yz) p (y 2 – zx) q = z 2 – xy are first order quasilinear partial differential equations Nonlinear equation A first order partial differential equation f(x, y, z, p, q) = 0 which does not come under the above three types, in known as a nonliner equationZ Z S F~ ·dS~ = R R D (−P ∂g ∂x − Q∂g ∂y R)dA = R1 0 R1 0 −(xy)(−2x)− (yz)(−2y)(zx)dxdy = R1 0 R1 0 −(xy)(−2x)− y(4−x2 − y2)(−2y)(4−x2 − y2)xdxdy R1 0 R1 0 4x− x3 2x2y 8y2 − xy2 − 2x2y2 −2y4dxdy = 713/180 Section177, #24Evaluate the surface integral

If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora

Find The Minimum Value Of X 2 Y 2 Z 2 Subject To The Conditions Xy Yz Zx 3a 2 Sarthaks Econnect Largest Online Education Community

Given x y z = 6, x2 y2 z2 = 10 x3 y3 z3 = 12 Formula used (x y z)2 = x2 y2 z2 2(xy yz zx) x Q1 Columbus started his journey from Lucknow to Kolkata which is 0 km, at the speed of 40 km/h then he went to Banglore which is 300 km at the speed of km/hThis gives an implicit formula of x 2 y 2 y 2 z 2 z 2 x 2 − r 2 x y z = 0 {\displaystyle x^ {2}y^ {2}y^ {2}z^ {2}z^ {2}x^ {2}r^ {2}xyz=0\,} Also, taking a parametrization of the sphere in terms of longitude (θ) and latitude (φ), gives parametric equations for the Roman surface as follows First We take RHS & use the Formula ( ab)²= a²b²2ab & simplify it then RHS becomes equal to LHS RHS ⇒ 1/2×(x y z) (x² y²2xy y² z²2yzx²z²2xz)

If X Y Z 5 And X 2 Y 2 Z 2 29 Find The Value Of Xy Yz Zx Brainly In

Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z

Neitherwaseven x=2h1and y=2k1 Then z 2=4h 4h14k2 4k1=4(h hk2 k)2 Thissaysthat2z2 but4 ∤ z2 whichisimpossiblebecause z2 isaperfectsquare Weshallchoose xtobeeven Theorem The triple (x,y,z) is a primitive Pythagorean triple if and only if there existtworelativeprimeintegers sand tsothat s > t >0and x=2st y= s2 −t2 and z= s2 t2X^22*x*yy^2z^2x^2y^2z^2–2*x*y2*x*z2*y*z= 2*z^22*x*z2*y*z which is not identically 0, so there are a set of points where the 2 expressions are equal (such as z=0 and z=xy) but in general they are not equal views View upvotes 9 Related Answer 19 x 2 y 2 z 2 − xy – yz –zx = 1/2(x − y) 2 (y − z) 2 (z − x) 2 Maths Algebraic Identities For Class 9 Do you know the difference between an algebraic formula (identity) and an algebraic expression?

Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx

Solved I Want The Detail Solution Thank You I Will You Chegg Com

An algebraic formula is an equation that is a rule written using mathematical and algebraic symbols (a b) 2 =a 2 Making m = xy n = yz p = xz we have m^2n^2p^2 = 2(x^2y^2z^2x*yx*zy*z) then x^2y^2z^2x*yx*zy*z = 1/2((xy)^2(yz)^2(xz)^2) Algebra ScienceX^2y^2z^2xyyzzx=0 multiplying the RHS and LHS by 2 we get , 2 x^2y^2z^2xyyzzx =0 or, (xy)^2(yz)^2(zx)^2=0 since in LHS there are only squared terms,ie they cannot be negative What are factors of 4x^212xy9y^24x6y35?

Solved Find A Normal Vector And An Equation For The Tangent Chegg Com

Factorise X 2 Y 2 Z 2 Xy Yz Zx

M4maths Previous Puzzles Which one statement is correct If x2 y2 z2 xy yz zx 0 then which one statement is correct OPtion 1) x = y = z 2) x > y > z 3) x y z 4) x ≠ y = z 5) x = y ≠ z 6) x ≠ y ≠ zP z Q O x y C D E Q(x2;y2;z2)is dist(P;Q)= q (x1¡x2) 2(y 1¡y2) 2(z 1¡z2) 2 We shall use the dimension reduction to verify this formula In the above &gure, we project point P and Q vertically (parallel to z ¡axiz) onto xy ¡Click here👆to get an answer to your question ️ Using the identity and proof x^3 y^3 z^3 3xyz = (x y z)(x^2 y^2 z^2 xy yz zx)

Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z

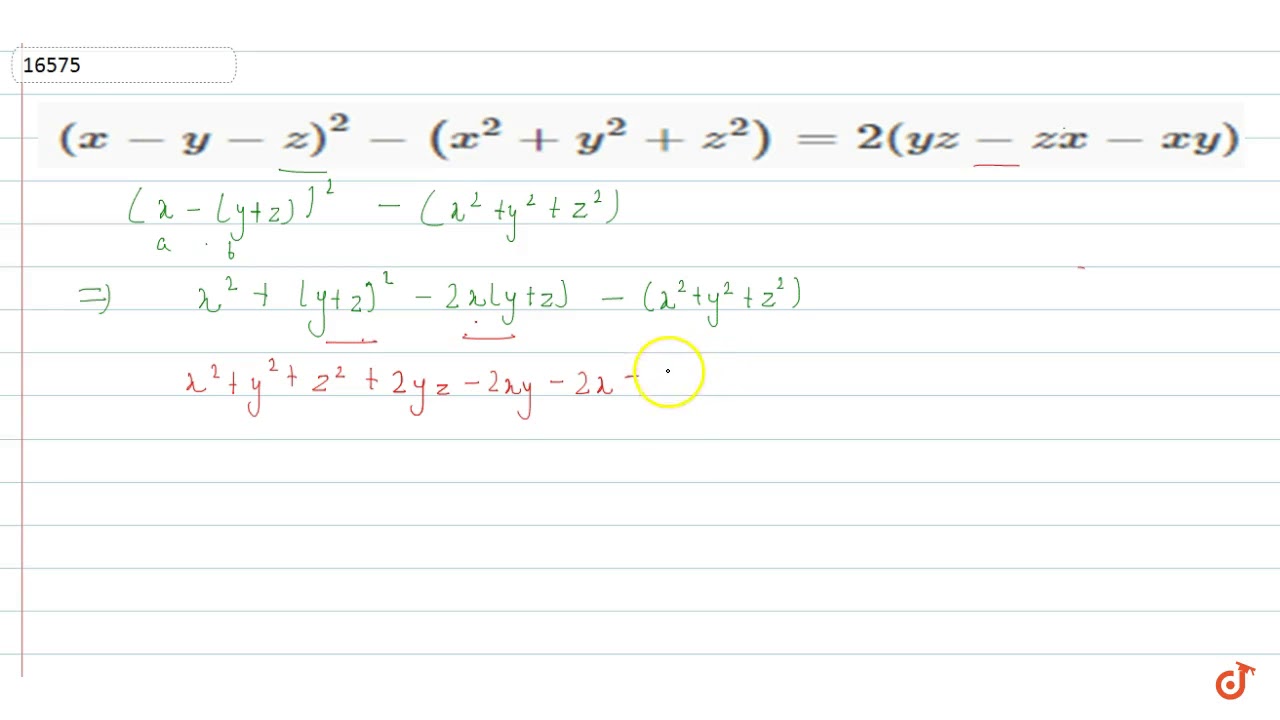
X Y Z 2 X 2 Y 2 Z 2 2 Yz Zx Xy Youtube

Answer (1 of 12) xyz=0, so xy= z; Example Ifu =x y z, v = x y2 z2 and w = yz zx xy prove that (grad u) {grad v x grad w} = 0 dear frist of all u solve grad U ,grad V ,grad W after thenu get further solutionwhich is already attached by others tutor then if x y z = 5 x 2 y 2 z 2 = 21 y 2 = zx Formula used (x y z) 2 = x 2 y 2 z 2 2(xy yz xz) Calculations (x y z) 2 = 5 2 ⇒ x 2 y 2 z 2 2(xy yz xz) = 25 ⇒ 21 2(xy yz xz) = 25 ⇒ 2(xy yz xz) = 25 21 ⇒ xy yz xz = 4/2 ⇒ xy yz xz = 2 ⇒ xy yz y 2 = 2 ⇒ y(x y z) = 2 ⇒ y(5) = 2 ⇒ y = 2/5

Prove That X 2 Y 2 Z 2 X Y Y Z Z X Is Always Positive

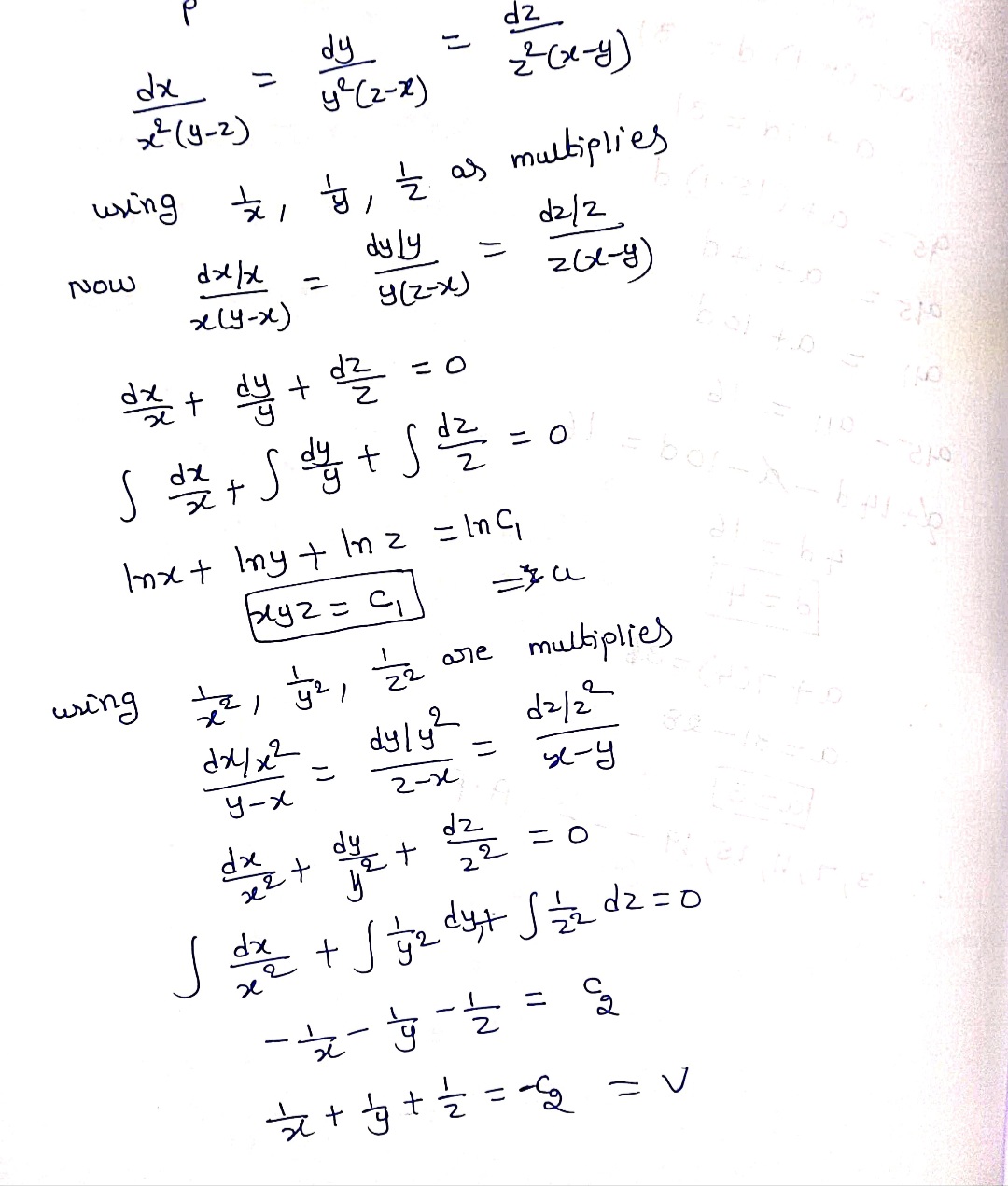
Answered Solve X2 Y Z P Y2 Z X Q Z2 X Y Bartleby

Xz= y = (x^2/yz) (y^2/xz) (z^2/xy) = x^2(xz)(xy) y^2(yz)(xy) z^2 (yz)(xz) / (yz)(xz)(xy) = x^2 (x^2yz) y^2 (xy^2z) z^2 (xyz^2) / x^2y^2z^2 = x^4yz xy^4z xyz^4 / x^2y^2z^2 = xyz (x^3 y^3 z^3) / (xyz)(xyz) = x^3#2 in 116 Find the equation of a tangent plane and the equation of a normal line to the surface x2 y2 z2 = 18 at the point P(3;5; Important Statistics Formulas (I) The Mean of Grouped Data can be found by 3 methods Direct Method formula This method can be very calculation intensive if the values of f and x are largeWe have big calculations and chance of making mistake is quite high 2 Assumed mean method formula Where a= Assumed mean and d i = x i –a This method is quite useful

How To Prove That Math X 2 Y 2 Z 2 Xy Yz Zx Math Is Always Positive Quora

Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z

How do I prove that x^2y^2z^2xyyzzx=1\2 ((xy) ^2(yz) ^2(zx) ^2)?We rst note that these planes intersect along the line x y= 1 It follows that the base of Eis a 2D region Dthat can be described by the inequalities x 0, y 0, and x y 1 Given x^2y^2z^2=xyyzzx (1)multiplying by (xyz) on both sidesx^2y^2z^2 (xyz)=(xyyzzx ) (xyz)expand the above equationsx^3y^3z^3xy^2x^2 yyz^2y^2 zxz^2x^2 z=x^2 yxyzzx^2xy^2 y^2 zxyzxyz

Solved Find The Integral Surface Of The Partial Differential Chegg Com

Prove That X2 Y2 Z2 Xy Yz Zx Is Always Positive Brainly In

Example 2 if x = 10 and y is 4 (10 4) 2 = 10 2 2·10·4 4 2 = 100 80 16 = 36 The opposite is also true 25 a 4a 2 = 5 2 2·2·5 (2a) 2 = (5 2a) 2 Consequences of the above formulas4) Let f = x2y2 z2 Then the surface is a level surface of f Therefore, the gradient of f at P is normal to the surface We compute this vector rf = h2x;2y;The formula of x 3 y 3 z 3 – 3xyz is written as \(x^{3} y^{3} z^{3} – 3xyz = (x y z) (x^{2} y^{2} z^{2} – xy – yz – zx)\) Let us prove the equation by putting the values of x = 1;

Partial Differential Equations Lagranges Linear Pde X 2 Y Z P Y 2 Z X Q Z 2 X Y Youtube

Solve The Equations X 2 Xy Xz 18 Y 2 Yz Yx 12 Z 2 Zx Zy 30 Youtube

(2) ∂f ∂z = lim ∆z→0 f(x,y,z ∆z)−f(x,y,z) ∆z (3) These formulae are direct generalisations of the well known definition of the derivative of a function f(x) of one variable x df dx = lim ∆x→0 f(x∆x)−f(x) ∆x (4) Example Let f(x,y,z) = x2yz yez, then ∂fF(x,y,z) = x2yz −xy2z decreases in the y direction (a) (1,−1,2), (b) (1,1,1), (c) (−1,1,2), (d) (1,0,1) Definition if nˆ is a unit vector, then nˆ·∇f is called the directional derivative of f in the direction nˆ The directional derivative is the rate of change of f in the direction nˆ11 Functions of Two or More Variables A symbol z which has a definite value for every pair of values of x and y is called a function of two independent variables x and y and is written as z = f (x, y) or I (x, y) 12 Limits "The function f (x, y) is said to tend to limit l as x oa and y o b if and only if the limit l is independent of the path followed by the point (x, y) as x o a and y ob

Multiply I X 2 Y 2 Z 2 Xy Xz Yz By X Y Z Ii X 2 4y 2 Z 2 2xy Xz 2yz By X 2y Z Sarthaks Econnect Largest Online Education Community

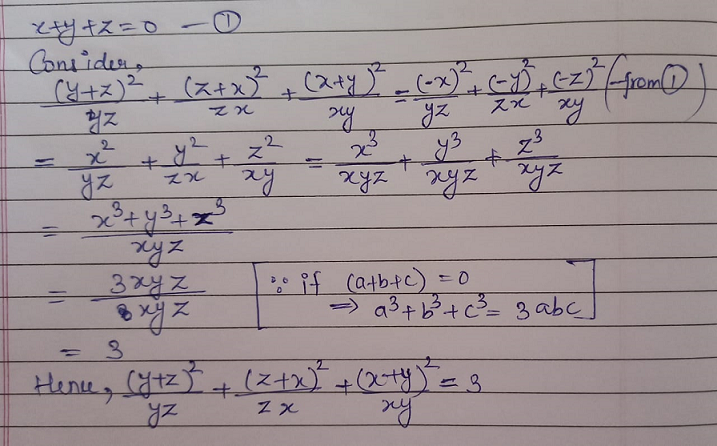
How To Solve If X Y Z 0 Find The Value Of Y Z 2 Yz Z X 2 Zx X Y 2 Xy Mathematics Topperlearning Com 7bcu50oo

X^2y^2z^2xyyzzx=0 multiplying the RHS and LHS by 2 we get , 2 x^2y^2z^2xyyzzx =0 or, (xy)^2(yz)^2(zx)^2=0 since in LHS there are Ex 42, 9 By using properties of determinants, show that 8 (x&x2&yz@y&y2&zx@z&z2&xy) = (x – y) (y – z) (z – x) (xy yz zx) Solving LHS 8 (𝑥&𝑥^2&𝑦𝑧@𝑦&𝑦^2&𝑧𝑥@𝑧&𝑧^2&𝑥𝑦) Applying R1→ R1 – R2 = 8 (𝑥−𝑦&𝑥^2−𝑦^2&𝑦𝑧−𝑥𝑧@𝑦&𝑦^2&𝑧𝑥@𝑧&𝑧^2&𝑥𝑦) Ex 42, 9 By using properties of determinants, show that 8 (x&x2&yz@y&y2&zx@z&z2&xy) = (x – y) (y – z) (z –(B)Factorize the polynomial using the factorization formula  10 1 6x 9x2 11 144x2 – 72x 9 12 4a2b2 abcd 25c2d2 13 x2 y2 – a2 – b2 2xy 2ab

Solved Find Equations Of A The Tangent Plane And B The Chegg Com

Answered 15 F X Y Z Xy Yz Zx Po 1 1 Bartleby

Or x = c 1 y ie, c 1 = x / y From the last two ratios, Integrating, log y = log z log c 2 or y = c2 z ie, c2 = y / z Hence the required general solution is Φ( x/y,= 0,y/z)where Φ is arbitrary Example 22 Solve p tan x q tan y = tan z The subsidiary equations are x2y2z2xyyzzx=0 However, the graph is a line x=y=z as can be seen by using the CauchySchwarz inequality (a12 an2)(b12 bn2) ≥ (a1b1 anbn)2 With equality happening if for all 1 ≤ k ≤ n, ak= bk In this case, take (a1,a2,a3) = (x,y,z) and (b1,b2,b3) = (y,z,x) (x2 y2 z2)(y2 z2 x2) ≥ (xy yz zx)2X^2y^2z^2xyyzzx formula X^2y^2z^2xyyzzx formulaFactor x^2y^2 x2 − y2 x 2 y 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = (a b) (a b) where a = x a = x and b = y b = y (xy)(x−y) (x y) (x y)(x y) 2 = x 2 y 2 2ab Therefore, we can write the above equation as;

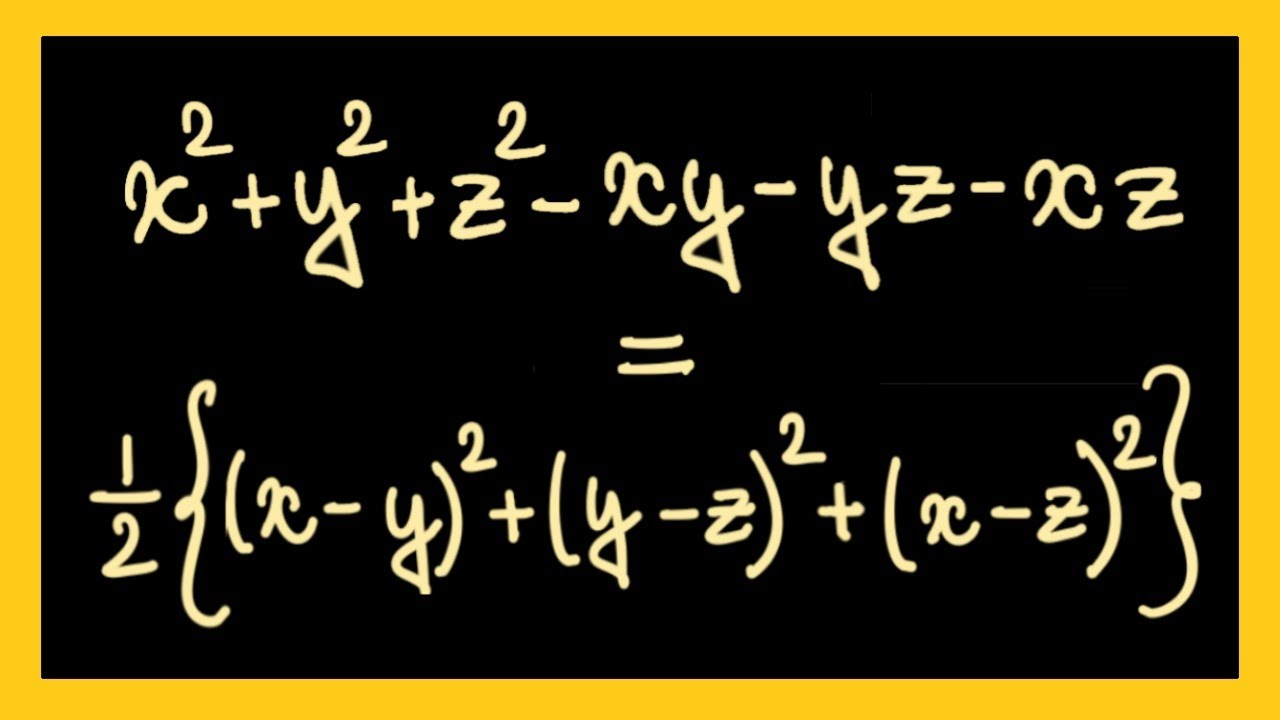
X2 Y2 Z2 Xy Yz Xz Formula X2 Y2 Z2 Xy Yz Xz Identity X Y Z Xy Yz Xz 1 2 X Y Y Z X Z Youtube

If X Y Z 0 Find Value Of Y Z 2 Yz Z X 2 Zx X Y 2 Xy Mathematics Topperlearning Com Y34sig11

 x2y2z2=xyyzzx you can get 2x22y22z2=2xy2yz2zx which equals 2x22y22z22xy2yz2zx=0,the equivalant is (xy)2(yz)2(zx)2=0If $xy yz zx = 1$, then show that $$\dfrac{x}{1x^2} \dfrac{y}{1y^2} \dfrac{z}{1z^2} = \dfrac{4xyz}{(1x^2)(1y^2)(1z^2)}$$ I tried doing the sum algebraically, that is, by solving Stack Exchange NetworkAlgebra Examples Rewrite (xy z)2 ( x y z) 2 as (xyz)(xyz) ( x y z) ( x y z) Expand (xyz)(xyz) ( x y z) ( x y z) by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply x x by x x Multiply y y by y y

Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5

When Using The Formula Zx X For The Z Score For The 11 7

= y z x y ¯ z x y z ¯ = x ( y X O R z) y z, so the formula is symmetric in permutations of x,y,z, and the expression is true at least whenever two of the variables are true However, it's fairly easy to see that it is false when at most one variable is true

Factorise X Y Z 4 2xy Yz Zx Brainly In

If X Y Z 6 And Xy Yz Zx 10 Then What Is The Solution Of X 3 Y 3 3xyz Mathematics Concepts

If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3

Arxiv Org

Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Give Step By Step Explanation It S Urgent Brainly In

Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Youtube

If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz Youtube

1

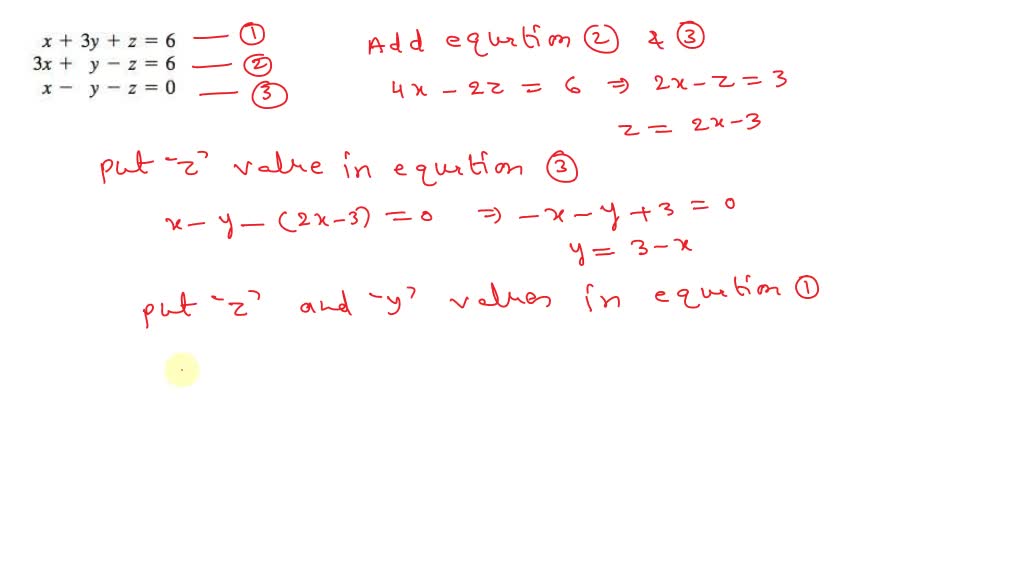
Solved Solve The Following X 2 Y 2 Z 2 Xy Xz Yz 6 0 Given That X Y And Z Do Not Equal 0

Find The Directional Derivative Of Xy 2 Yz 2 Zx 2 Along The Tangent To Curve X T Y T 2 Z T 2 At 1 1 1 Mathematics Is Life

Factorise X 2 Y 2 Z 2 Xy Yz Zx Youtube

What Is The Way To Factorize X 2 Y 2 Z 2 Xy Yz Zx Quora

If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3 Youtube

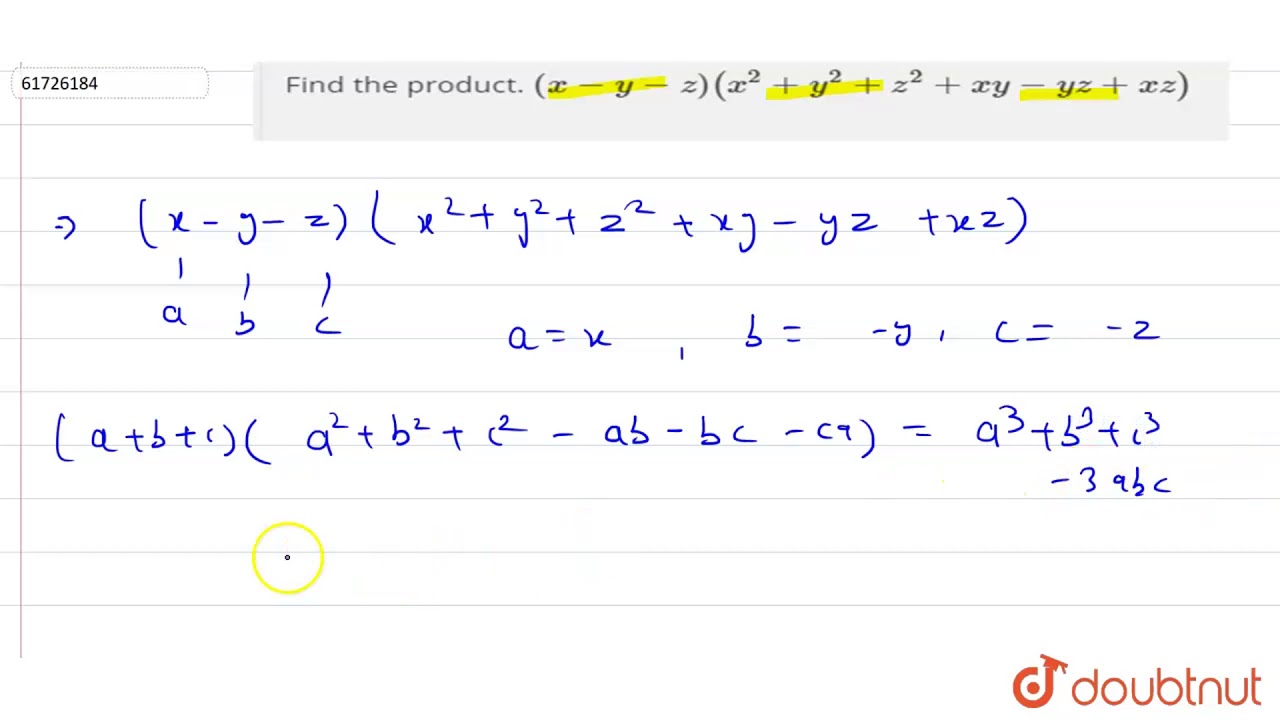
Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Xz Youtube

X2 Y2 Z2 24 Nd Xy Yz Zx Find X Y Z Brainly In

Unomaha Edu

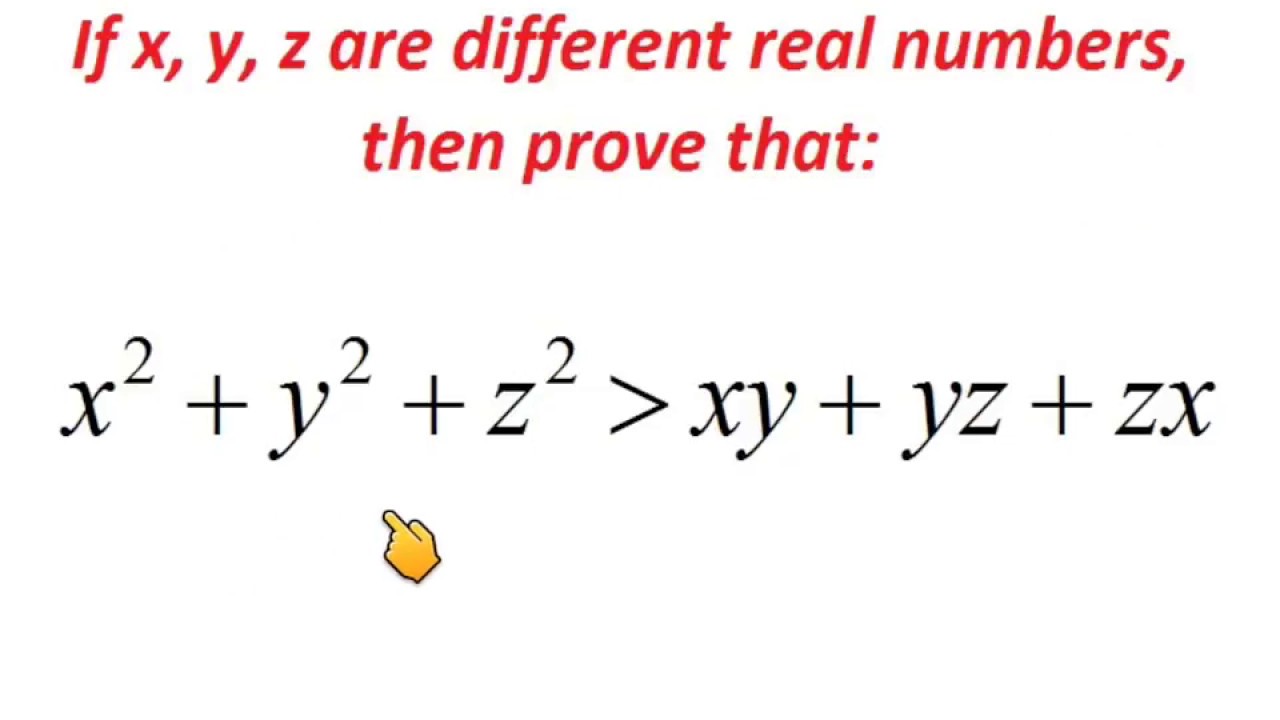
X 2 Y 2 Z 2 Greater Than Xy Yz Xz Proof Important For Iit Jee Nda Scra Sat Competitive Exams Youtube

If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3 Youtube

Show That The Functions U X Y Z V Xy Yz Zx And W X 3 Y 3 Z 3 3xyz Are Independent And Find The Relation Between Them Mathematics

Show That X3 Y3 Z3 3xyz X Y Z X2 Y2 Chegg Com

If X Y Z 2 Xy Yz Zx 11 And Xyz 12 Then What Is The Value Of X 3 Y 3 2 Quora

Solve A System Of Non Linear Equation Docx

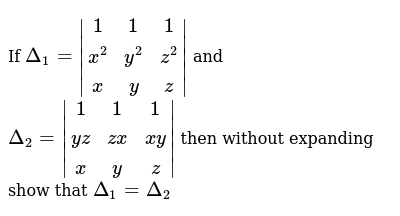
If Delta 1 1 1 1 X 2 Y 2 Z 2 X Y Z And Delta 2 1 1 1 Yz Zx Xy X Y Z Then Without Expanding Show That Delta 1 Delta 2

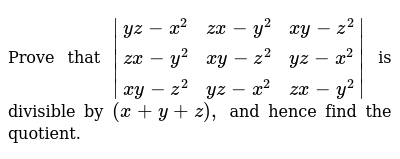
Prove That Yz X 2 Zx Y 2 Xy Z 2 Zx Y 2 Xy Z 2 Yz X 2 Xy Z 2 Yz X 2 Zx Y 2 Is Divisible By X Y Z And Hence Find The Quotient

Solved Problem 1 Find Equations Of The Tangent Plane And The Chegg Com

Solved F X Y Z X 2y Y 2z Xz 2 Partial Differential Chegg Com

Ualberta Ca

X 2 Y 2 Z 2 100 Xy Yz Zx 2 Brainly In

Solved Find The Integral Surface Of The Partial Differential Equation 2xy 1 P Z 2x3 Q 2 X Yz Through Curves X 1 And Y 0 Course Hero

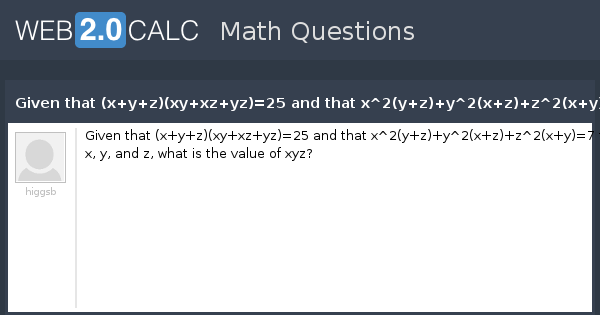
View Question Given That X Y Z Xy Xz Yz 25 And That X 2 Y Z Y 2 X Z Z 2 X Y 7 For Real Numbers X Y And Z What Is The Value Of Xyz

Se Cse Pde Pages 1 17 Flip Pdf Download Fliphtml5

Ppt Polynomials Powerpoint Presentation Free Download Id

Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx

If X Y Z 9 And X Y Y Z X Z 26 Find The Value Of X2 Y2 Z2 Brainly In

X Y Z Belong To R X Y Z 4 X 2 Y 2 Z 2 6 Find Maximum Possible Value Of Z Mathematics Topperlearning Com 2j1z7sww

If X Y And Z Are Real Numbers Such That X Y Z 1 Then What Is The Value Of Xy Yz Xz Quora

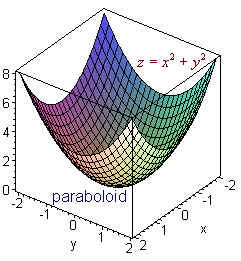
Surfaces

Solved Solve Yz 2 X 2 Yz Dx Zx 2 Y 2 Xz Dy Xy 2 Z 2 Xy Dz 0 Subject Differential Equation And Integral Equation Course Hero

What Are X Y And Z If X 2 Xy Y 2 7 Y 2 Yz Z 2 13 And Z 2 Xz X 2 19 Quora

Solved Solve Yz 2 X 2 Yz Dx Zx 2 Y 2 Xz Dy Xy 2 Z 2 Xy Dz 0 Subject Differential Equation And Integral Equation Course Hero

Solved 3 Consider The Following Function F X Y Z Xy Chegg Com

Find The Directional Derivative Of F X 2yz 4xz Xyz At 1 2 3 In The Direction Of Vector 2i J K Sarthaks Econnect Largest Online Education Community

2 101 2 X 2 10 1 Y 0 1 2 3 4 Z

X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube

If X Y Z 1 X 2 Y 2 Z 2 Xy Yz Zx 18 What Is Value Of X Y Z Quora

If X2 Y2 Z2 Xy Yz Xx O Prove That X Y Z Maths Polynomials Meritnation Com

Factorise X 2 Y 2 Z 2 Xy Yz Zx

Tangent Plane To X 2 Xy Y 2 Z 0 Youtube

Polynomials Ppt Video Online Download

How To Solve Cyclic Differential Equations

1

Pdf Extrema Of Xy Yz Zx When X Y Z And Xyz Are Constant

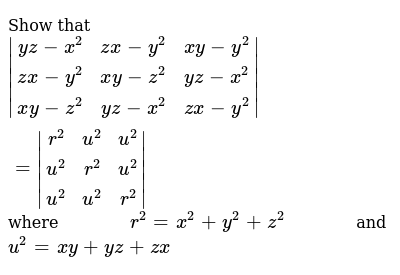
Show That Yz X 2 Zx Y 2 Xy Y 2 Zx Y 2 Xy Z 2 Yz X 2 Xy Z 2 Yz X 2 Zx Y 2 R 2 U 2 U 2 U 2 R 2 U 2 U 2 U 2 R 2 Where R 2 X 2 Y 2 Z 2 And U 2 Xy Yz Zx

Let Math X 2 Y Z Y 2 Z X Z 2 X Y Math What Is The Value Of Math Frac 1 1 X Frac 1 1 Y Frac 1 1 Z Math Quora

Show That The Equation X 2 Y 2 Z 2 X Y Y Z Z X Has Infinitely Many Solutions In Integers X Y Z M Cube Mathematics By Maheshwari

Jacobian If U Xyz V X 2 Y 2 Z 2 W X Y Z Find J X Y Z U V W Youtube

X3 Y3 Z3 3xyz

Factorising Cyclic Expression X 2 Y Z Y 2 Z X Z 2 X Y Youtube

A Rigid Body Rotates About An Axis Through The Origin With An Angular Velocity 10v3 Radians Sec If W Points In The Direction Of I Then The Equation To The Locus Of The

If X 2 Y 2 Z 2 1 Then Xy Yz Zx Lies In

Solved 9 Draw The Xy Xz Yz Traces For The Following Chegg Com

Factorize 1 X Y Z Xy Yz Zx Xyz Youtube

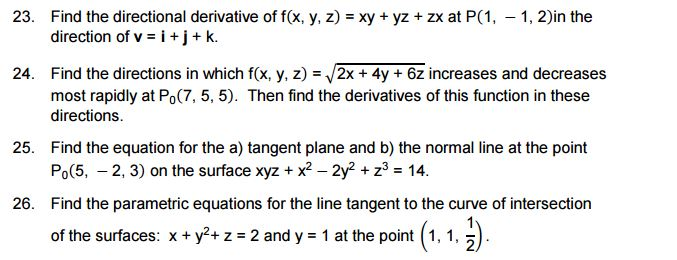
Solved 23 Find The Directional Derivative Of F X Y Z Chegg Com

Http Www Aplustopper Com Solving A Quadratic Equation By Factoring Maths Solutions Quadratics Quadratic Equation

Consider Z Sqrt X 2 Y 2 Give The Domain And Range Draw The Zx And Zy Traces In Two Homeworklib

X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In

X Y Z X2 Y2 Z2 Xy Yz Zx Is This Any Formula Brainly In

Answered Solve X2 Y Z P Y2 Z X Q Z2 X Y Bartleby

How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube

Solved Solve Yz 2 X 2 Yz Dx Zx 2 Y 2 Xz Dy Xy 2 Z 2 Xy Dz 0 Subject Differential Equation And Integral Equation Course Hero

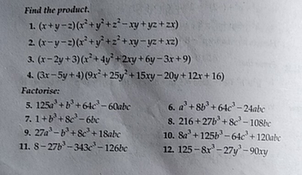
Find The Product 1 X Y Z X2 Y2 Z2 Xy Yz Zx 4 Gr Scholr

Mathematics Class 9th Chapter 4 Solution

Surfaces Part 2

How To Show That The Cone Yz Zx Xy 0 Cuts The Sphere X2 Y2 Z2 A In Two Equal Circles And What Is Their Area Quora

If Xy Yz Zx 1 Prove That X 1 X 2 Y 1 Y 2 Z 1 Z 2 4 Xyz 1 X 2 1 Y 2 1 Youtube

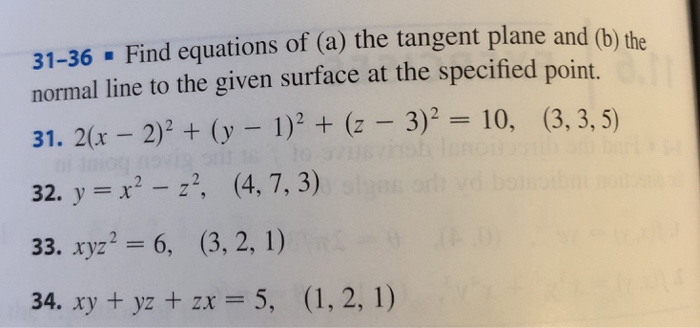
Solved 31 36 Find Equations Of A The Tangent Plane And B Chegg Com